Calculate Nonparametric 95% Reference Interval

calc.reference.interval <- function(val, wgt)
{
    ## Purpose: Calculate Nonparametric 95% Reference Interval. 
    ## Notes: 
    ##    1) Each Reference Interval needs at least 120 reference observations (per CLSI C28-A3c).
    ##    2) A general criterion for determining sample size is that the width of the 90% confidence interval (CI)
    ##       for a reference limit should be acceptably small relative to the width of the 95% reference interval
    ##       itself (Harris and Boyd); these authors recommend that the width of the 90% CI be less than 0.2 times
    ##       the width of the reference interval. 
    ## Arguments:
    ##   val: numerical measurements
    ##   wgt: weight (frequency) of these measurements
    ## Return: a Nonparametric 95% Reference Interval. 
    ## Author: Feiming Chen
    ## ________________________________________________

    x <- rep(val, wgt)
    cat("N =", length(x), "\n")
    cat("Reference Interval:\n")
    print(q <- quantile(x, probs = c(0.025, 0.975)))

    ## Confidence Intervals for the Nonparametric Method (Using Bootstrap with 2000 Reps)
    require(boot)
    b <- boot(x, 
              function(x, i) {
                  quantile(x[i], probs = c(0.025, 0.975))
              }, R = 2000)

    cat("\n90% Bootstrap CI for Lower 95% Reference Limit:")
    L <- boot.ci(b, conf=0.90, type="basic", index=1)
    print(L2 <- L$basic[1,c(4,5)])

    cat("\n90% Bootstrap CI for Upper 95% Reference Limit:")
    U <- boot.ci(b, conf=0.90, type="basic", index=2)
    print(U2 <- U$basic[1,c(4,5)])

    cat("\nRatio of Limit CI Width to Reference Interval Width (Recommend: < 0.2):\n")
    q2 <- diff(q)                       # Width of Reference Interval
    L3 <- diff(L2)                      # Width of Lower Limit 90% CI
    U3 <- diff(U2)                      # Width of Upper Limit 90% CI
    cat("Lower Limit CI Width Ratio:", round(L3 / q2, 3), "\n")
    cat("Upper Limit CI Width Ratio:", round(U3 / q2, 3), "\n")

    list(Reference.Limit = q, 
         Lower.Limit.CI = L2,
         Upper.Limit.CI = U2)
}
if (F) {                                # Unit Test
    ## Data from CLSI C28-A3c (Reference Interval) Table 4 (Frequency Distributions of Calcium in 240 Medical Students by Sex)
    ## Only Women's Data. CLSI Reported "Nonparametric" Method: N = 120, Calcium.Women = (8.9, 10.2),
    ##                    Lower Limit 90% CI = (8.8, 9.1), Upper Limit 90% CI = (10.1, 10.3)
    val <- c(8.8,8.9,9.0,9.1,9.2,9.3,9.4,9.5,9.6,9.7,9.8,9.9,10.0,10.1,10.2,10.3,10.4,10.5,10.6)
    wgt <- c(1,2,1,3,11,11,8,16,16,26,8,7,3,2,3,2,0,0,0)
    ans <- calc.reference.interval(val, wgt)
    ##   2.5%   97.5% 
    ## 8.9975 10.2000 
}

Variance Component Analysis for One-Way Random Model

var.comp.one.way.model <- function(fmla, dat)
{
    ## Purpose: Variance Component Analysis for One-Way Random Model. 
    ##          Application: Repeatability and Reproducibility Analysis (R&R for Precision Study).
    ##          Use Method of Moment estimation.  
    ## Arguments:
    ##    fmla: a formula with one response and one factor (One-way Random Model).
    ##    dat: a data frame
    ## Return: Variance Component Analysis such as
    ##         DF: Degrees of Freedom
    ##         VC: Variance Component (with proportion of total in percentage)
    ##         SD: Standard Deviation (from the squared root of Variance Component)
    ##         CV%: Coefficient of Variation as Percentage
    ## Author: Feiming Chen
    ## ________________________________________________

    a <- aov(fmla, dat)
    b <- summary(a)
    cat("Analysis of Variance:\n")
    print(b)                   # Analysis of Variance
    MEAN <- mean(a$model[[1]])  # Mean 
    N <- nrow(a$model)          # Number of observations
    cat("\nMean: ", round(MEAN, 3), " (N =", N, ")\n", sep="")
    
    d <- b[[1]]
    VC.error <- d$"Mean Sq"[2]          # Mean Sum of Squares for Error = Variance Component for Error (Repeatability)
    Q2 <- d$"Sum Sq"[1]                 # Sum of Squares for Treatment
    DF.treatment <- d$Df[1]             # DF for Treatment
    N.i <- table(a$model[[2]])          # Number of Replicates in Each Treatment Choice
    VC.treatment <-  (Q2 - DF.treatment * VC.error) / (N - sum(N.i^2) / N)

    VC <- c(VC.treatment, VC.error, VC.treatment + VC.error)
    VC.pct.total <- VC / VC[3] * 100
    SD <- sqrt(VC)
    CV.pct <- SD / MEAN * 100
    
    ans <- data.frame(Name = c(attr(a$terms, "term.labels"), "Error", "Total"), 
                      VC = round(VC, 3), 
                      VC.Pct.Total = round(VC.pct.total, 3), 
                      SD = round(SD, 3), 
                      CV.Pct = round(CV.pct, 3))

    cat("\nVariance Component Analysis:\n")
    ans
}
if (F) {                                # Unit Test
    dat <- data.frame(Yield=c(3.9, 4.05, 4.25, 3.60, 4.2, 4.05, 3.85, 4.15, 4.6, 4.15, 4.4, 3.35, 3.8), 
                      Variety=factor(c(1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 4, 4)))
    fmla <- Yield ~ Variety
    var.comp.one.way.model(fmla, dat)

    ## Validation
    library(VCA)
    anovaVCA(fmla, dat)
}

Compare the speed of product vs exp/sum/log calculations

## Compare the speed of product vs exp/sum/log calculations

library(microbenchmark)
x <- runif(1000) + 0.5
all.equal(prod(x), exp(sum(log(x))))
## [1] TRUE                                

microbenchmark::microbenchmark(
                    prod(x), 
                    exp(sum(log(x)))
)

## Unit: microseconds
##             expr    min     lq     mean  median      uq     max neval
##          prod(x)  2.075  2.107  2.52904  2.1945  2.5285  13.964   100
## exp(sum(log(x))) 51.525 52.075 62.89344 52.6135 62.5120 400.676   100

We can see it is much faster to use the straightforward calculation of "prod".

Use R Environment Object to Share and Modify (Big) Data Within Functions

We can use the R environment object just like a list.  One advantage is that it will be passed by reference to functions.  So it can be modified inside functions without the need to make additional copies.  Refer to Environment for more detailed explanation.  Following is an example usage.

## Use Reference Semantics to pass data object to functions by reference.
dat <- new.env(parent = emptyenv())

## Put in some data
dat$iris <- iris
dat$cars <- cars

## Checking the original object. 
ls(dat)                                
## [1] "cars" "iris"

## An example function
f <- function(d) d$N <- nrow(d$iris) + nrow(d$cars)

## Passing the data by reference: It can be modified inside the function.
f(dat)

## Checking the modified object. 
ls(dat)                                
## [1] "cars" "iris" "N"   
dat$N
## [1] 200
identical(dat$N, nrow(dat$cars) + nrow(dat$iris))
## [1] TRUE

## In practice, we can use f1(dat), f2(dat), f3(dat), ...
## to continuously update the information/states maintained in "dat".

Examining R Profiling Data

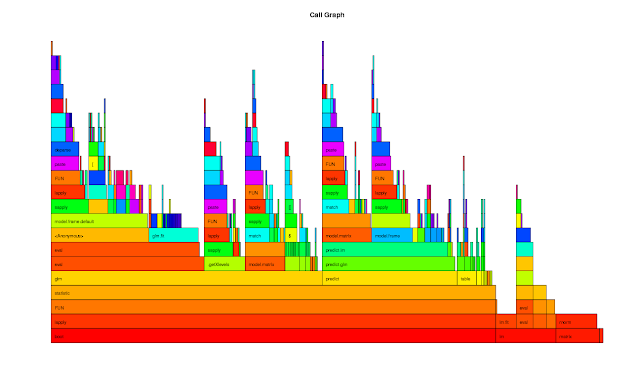
rprof <- function(srcfile)
{ 
    ## Purpose: R Profiling with R "proftools" package. 
    ## Arguments:
    ##   srcfile: path to source file. 
    ## Return: plots and summary of profiling. 
    ## Author: Feiming Chen, Date: 23 May 2018, 10:31
    ## ________________________________________________

    library(proftools)
    pd0 <- profileExpr(source(srcfile))
    pd <- filterProfileData(pd0, select = "withVisible", skip = 4)

    cat("\nSummarize by function -------------------------------------\n")
    print(head(funSummary(pd, srclines = FALSE), 10))

    cat("\nSummarize by call -----------------------------------------\n")
    print(head(callSummary(pd), 10))

    cat("\nHot Execution Paths ---------------------------------------\n")
    print(hotPaths(pd, total.pct = 10.0))

    plotProfileCallGraph(pd, maxnodes = 15)

    flameGraph(pd)

    calleeTreeMap(pd)

    pd
}
if (F) {                                # Unit Test
    srcfile <- system.file("samples", "bootlmEx.R", package = "proftools")
    rprof(srcfile)
}

The output of the Unit Test is as follows:

Summarize by function -------------------------------------
                    total.pct gc.pct self.pct gcself.pct
statistic               80.57   7.21     0.66       0.00
lapply                  80.57   7.21     1.75       0.00
FUN                     80.57   7.21     1.97       0.44
boot                    80.57   7.21     0.00       0.00
glm                     49.13   5.24     0.87       0.22
eval                    32.75   1.97     1.97       0.22
model.frame.default     27.51   1.75     1.31       0.00
sapply                  26.42   3.06     0.87       0.00
predict                 24.45   1.53     0.44       0.00
predict.glm             24.02   1.53     0.44       0.00

Summarize by call -----------------------------------------
                                       total.pct gc.pct self.pct gcself.pct
lapply -> FUN                              80.57   7.21     1.09       0.22
FUN -> statistic                           80.57   7.21     0.66       0.00
statistic -> glm (bootlmEx.R:33)           49.13   5.24     0.87       0.22
boot (bootlmEx.R:39) -> lapply             38.21   3.93     0.00       0.00
boot (bootlmEx.R:44) -> lapply             37.55   3.06     0.00       0.00
eval -> eval                               30.13   1.97     0.87       0.22
glm (bootlmEx.R:33) -> eval                27.73   1.75     0.87       0.00
statistic -> predict (bootlmEx.R:35)       24.45   1.53     0.44       0.00
predict (bootlmEx.R:35) -> predict.glm     24.02   1.53     0.44       0.00
sapply -> lapply                           23.14   3.06     1.75       0.00

Hot Execution Paths ---------------------------------------
 path                            total.pct self.pct
 boot (bootlmEx.R:39)            38.21     0.00    
 . lapply                        38.21     0.00    
 . . FUN                         38.21     0.00    
 . . . statistic                 38.21     0.00    
 . . . . glm (bootlmEx.R:33)     24.67     0.44    
 . . . . . eval                  13.76     0.44    
 . . . . . . eval                13.32     0.22    
 . . . . predict (bootlmEx.R:35) 12.23     0.00    
 . . . . . predict.glm           12.01     0.44    
 . . . . . . predict.lm          11.35     0.22    
 boot (bootlmEx.R:44)            37.55     0.00    
 . lapply                        37.55     0.00    
 . . FUN                         37.55     0.00    
 . . . statistic                 37.55     0.00    
 . . . . glm (bootlmEx.R:33)     24.45     0.44    
 . . . . . eval                  13.97     0.44    
 . . . . . . eval                13.54     0.00    
 . . . . predict (bootlmEx.R:35) 12.23     0.22    

 . . . . . predict.glm           12.01     0.00    
 . . . . . . predict.lm          11.35     0.44    
 lm (bootlmEx.R:52)              10.92     0.00    

Predict with a Classification Tree ("rpart") Model

report.model.rpart <- function(fmla, dat, main = "Classification Tree")
{ 
    ## Purpose: Report a Classification Tree ("rpart") model and make plots.
    ##          Assume the response is a categorical variable (factor).
    ##          Require package "rpart" and "rpart.plot". 
    ## Arguments:
    ##   fmla: formula for the predictive model
    ##   dat: data frame for the training data
    ##   main: Title for the plot
    ## Return: 
    ## Author: Feiming Chen, Date: 18 May 2018, 11:41
    ## ________________________________________________

    library(rpart)
    library(rpart.plot)

    ans <- rpart(fmla, dat)

    rpart.plot(ans, main = main)

    mf <- model.frame(fmla, dat)
    Response <- factor(model.response(mf))                  # extract response

    Predicted.Response <- factor(predict(ans, type = "class"))
    err.mis(Response, Predicted.Response, file="Tree-Model-CART")

    if (nlevels(Response) == 2) {
        H0.label <- levels(Response)[1]
        o1 <- sens.spec(Response, Predicted.Response, H0=H0.label)
        print(o1)

        o2 <- sens.spec(Response, Predicted.Response, H0=H0.label, get.ppv = TRUE)
        print(o2)
    }

    ans
}
if (F) {                                # Unit Test
    data(iris)
    report.model.rpart(Species ~ ., iris) # Predict 3 species
    report.model.rpart(Species ~ ., subset(iris, Species != "setosa")) # Predict 2 species
}

Unit Test 1: Predict 3 Species

Unit Test 2: Predict 2 Species

Make a ROC plot with possible cutoff points

roc.curve <- function(response, predicted, cutoff = c(seq(0.1, 0.9, 0.1), 0.45, 0.55), ...) {
    ## Purpose: Make a ROC plot with possible cutoff points.
    ##          Require R package "ROCR"
    ## Arguments:
    ##    response: a vector of truth (0/FALSE/"negative" or 1/TRUE/"positive")
    ##    predicted: a vector of prediction (continuous);
    ##    cutoff: a list of values to be plotted on ROC curve.
    ##    ...: passed to "plot". 

    ## Return: a ROC plot.
    ## Author: Feiming Chen, Date: 14 May 2018, 15:01
    ## ________________________________________________

    require(ROCR)
    ans <- ROCR::prediction(predicted, response)
    ## ROC for Sensitivity vs. Specificity.
    plot((pp <- ROCR::performance(ans, "sens", "spec")), colorize=T,
         print.cutoffs.at=cutoff, text.adj=c(1.2, 1.2), text.cex=0.7, lwd=2,
         ...)
    grid(col="orange")

    ## Draw a "line of no-discrimination".
    ## Sens = P(X=+ | T=+), Spec = P(X=- | T=-),
    ## if X is independent of T, then Sens + Spec = P(X+)+P(X-) = 1, so the pair
    ## (Sens, Spec) lies on a off-diagonal line.
    abline(c(1, -1), col="gray70", lty=2)
    return(invisible(pp))
}
if (F) {
    roc.curve(rep(c(0,1), 50), runif(100), main = "ROC Curve Test")
}

Calculate the sample size required for detecting at least one rare event

sample.size.for.rare.event.detection <- function(alpha = 0.05, M = 0.01)
{ 
    ## Purpose: Calculate the sample size required for detecting at least one rare event. 
    ## Arguments:
    ##   alpha: Type I Error. Sensitivity = 1 - alpha.
    ##   M: Probability for the rare event. Default to 1%. 
    ## Return: A minimum sample size required for the detection of rare event
    ##         with (1-alpha) probability (aka. confidence). 
    ## Author: Feiming Chen, Date:  8 May 2018, 10:36
    ## ________________________________________________

    N <- ceiling(log(alpha) / log(1 - M))
    N
}
if (F) {                                # Unit Test
    sample.size.for.rare.event.detection() # 299

    ## Detecting 0.5% event with 99% confidence
    sample.size.for.rare.event.detection(alpha = 0.01, M = 0.005) # 919
}

Below is an application example.

Calculate the entropy of a signal emulating the classic Shannon definition.

signal.entropy <- function(x)
{ 
    ## Purpose: Calculate the entropy of a signal, emulating the classic Shannon definition. 
    ## Arguments:
    ##   x: A signal vector
    ## Return: An entropy number
    ## Author: Feiming Chen, Date:  1 May 2018, 13:07
    ## ________________________________________________

    x2 <- x^2
    tot <- sum(x2) 
    if (tot == 0) {
        H <- NA
    } else {
        p <- x2 / tot
        H <- - sum(p * log10(p))
    }
    H
}
if (F) {                                # Unit Test
    x <- rnorm(100)
    signal.entropy(x)
    signal.entropy(rep(1,100))          # 2
    signal.entropy(rep(1,10000))        # 4
}

Calibration Plot for Probability Prediction

calibration.plot <- function (y, p, main="Calibration Plot")  
{
    ## Purpose: Calibration Plot for Probability Forecast
    ## Arguments: 
    ##   y: the observed binary outcomes (0-1 response).
    ##   p: the probability forecasts (estimating E(Y|X)). 
    ## Return: 
    ##    - Calibration Plot
    ##    - A (Calibration-in-the-Large), and B (Calibration-Slope)
    ## Author: Feiming Chen
    ## ________________________________________________

    ## Fit Non-parametric model 
    newp <- seq(0, 1, length=100)
    yy <- predict(loess(y ~ p, span=1), newp, se=T) # LOESS Smoothing
    yy.ok <- !is.na(yy$fit)
    yy$fit <- yy$fit[yy.ok]             # calibration curve
    yy$se.fit <- yy$se.fit[yy.ok]       # standard error
    newp <- newp[yy.ok]
    se.lower <- yy$fit - 2 * yy$se.fit  # confidence band (lower limit)
    se.upper <- yy$fit + 2 * yy$se.fit  # confidence band (upper limit)

    ## Fit logist regression and obtain the intercept and slope
    dat <- data.frame(y = y, x = log(p / (1 - p)))
    f <- glm(y ~ x, family = binomial, data = dat) # "Cox, 1958, Biometrika"
    ce <- round(coef(f), 2)
    A <- ce[1]                          # A = Intercept
    B <- ce[2]                          # B = Slope 
    cf <- round(confint(f), 2)          # 95% CI 

    par(pty="s")
    plot(c(0,1), c(0,1), type="n", xlab="Predicted Probability",
         ylab="Observed Frequencies", xaxs="i", yaxs="i", las=1, main=main)
    polygon(c(newp, rev(newp), newp[1]), # plot confidence band
            c(se.lower, rev(se.upper), se.lower[1]), col = "gray", border = NA)
    rug(p[y == 0], side=1, col="navy")  # binary response 0's
    rug(p[y == 1], side=3, col="navy")  # binary response 1's
    abline(0, 1, col="red")             # perfect calibration line
    abline(h=0.5, col="red", lty=2)     # perfect irrelevance (no-discriminatino) line
    abline(v=0.5, lty=2)                # default cut-off at 50% for call
    lines(newp, yy$fit, lwd=2, col="blue") # plot calibration curve
    text(0.2, 0.8, labels = paste("A = ", A, "(", cf[1,1], ",", cf[1,2], ")"))
    text(0.2, 0.77, labels = paste("B = ",B, "(", cf[2,1], ",", cf[2,2], ")"))
    par(pty="m")
}
if (F) {                                # Unit Test
    calibration.plot(y = rbinom(1000, 1, 0.5), p = runif(1000), main = "Random Prediction")
    p <- runif(1000)
    y <- sapply(p, function(x) rbinom(1, size = 1, prob = x)) # perfect probability prediction
    calibration.plot(y, p, main = "Perfect Prediction")
}

R Analysis Report with Emacs Org Mode

Write a test.org file as follows:

* Test
You can write inline expressions like \pi = src_R{pi}.

Here is a code chunk.
#+NAME:foo
#+begin_src R :file plot.png :exports both :results output graphics
  x <- rnorm(100)
  summary(x)
  plot(x)
#+end_src

Export to HTML file (1st image) with C-c C-e h o
Export to PDF file (2nd image) with C-c C-e l o

R Analysis Report with Sweave/Knitr + Emacs + AUCTEX

1. In Emacs, compose a file "test.Rnw". 

\documentclass{article}  
\title{Test}
\begin{document}  

You can write inline expressions like $\pi=\Sexpr{pi}$.

Here is a code chunk.
<<a>>=
x <- rnorm(100)
summary(x)
plot(x)
@ 

\end{document}

2. Enter command for knitting: "M-n r" (Noweb => Sweaving/Tangling => Knit)
3. Enter command for generating PDF report: "M-n P". 
4. 

Equivalence Test for Two Means by TOST (Two One-Sided Test) Procedure

mean.equiv.tost.test <- function(x, y, margin=1, alpha=0.05) {
  ## Equivalence Test for Two Means by TOST (Two One-Sided Test) Procedure
  ## Assumption: Normality. 
  ## Reference: Understanding Equivalence and Noninferiority Testing (Walker and Nowacki)
  ## INPUT:
  ##    x: a vector of continuous scale.
  ##    y: another vector of continuous scale (to compare with x)
  ##    margin: Equivalence Margin (defaul to 1)
  ##    alpha: Significance Level.
  cl <- 1 - 2 * alpha
  a <- t.test(x, y, conf.level=cl)
  ci <- a$conf.int

  print(a)

  cat("Equivalence Test for Two Means by TOST Procedure:\n")
  cat("Equivalence Margin =", margin, "\n")

  if (ci[1] >= -margin && ci[2] <= margin) {
    cat("Equivalence Established! (Significance Level =", 100*alpha, "%)\n\n")
  } else cat("Equivalence NOT Established. (Significance Level =", 100*alpha, "%)\n\n")

  plot(0, 0, xlim=c(-2*margin, 2*margin), ylim=c(-1,1), axes=F, xlab="Difference in Efficacies", ylab="", type="n")
  axis(side=1, at=c(-2*margin, -margin, 0, margin, 2*margin), labels=c("", paste("-", margin), "0", margin, ""))
  abline(v=c(-margin, 0, margin), lty=c(2,1,2))
  lines(ci, c(0,0), lwd=3)
  lines(rep(ci[1], 2), c(-0.1, 0.1), lwd=2)
  lines(rep(ci[2], 2), c(-0.1, 0.1), lwd=2)
  lines(rep(-diff(a$estimate), 2), c(-0.1, 0.1), lwd=4)
}
if (F) {
  mean.equiv.tost.test(rnorm(20), rnorm(20, mean=0.3))
}

Equivalence Test for Proportions by TOST (Two One-Sided Test) Procedure

prop.equiv.tost.test <- function(x, n, margin=0.2, alpha=0.05) {
  ## Equivalence Test for Proportions by TOST (Two One-Sided Test) Procedure 
  ## Reference: Understanding Equivalence and Noninferiority Testing (Walker and Nowacki)
  ## INPUT:
  ##    x: a vector of two success counts,
  ##    n: a vector of two sample sizes
  ##    margin: Equivalence Margin (defaul to 20%)
  ##    alpha: Significance Level.
  cl <- 1 - 2 * alpha
  a <- prop.test(x, n, conf.level= cl)

  ## Using Score Interval for Difference of Proportions
  require(PropCIs)
  b <- diffscoreci(x[1], n[1], x[2], n[2], conf.level= cl)
  ci <- b$conf.int

  cat("\nEquivalence Test for Proportions by TOST Procedure:\n")
  cat("1st Trial =", x[1], "/", n[1], "=", round(x[1]/n[1]*100, 1), "% ,  2nd Trial =", x[2], "/", n[2], "=", round(x[2]/n[2]*100, 1), "%\n")
  pdiff <- -diff(a$estimate)            # p1 - p2
  cat("Difference in Efficacies =", 100 * round(pdiff, 3), "%\n")
  cat(100*cl, "% Confidence Interval = [", 100*round(ci[1], 3), "% ,", 100*round(ci[2], 3), "% ]\n")
  cat("Equivalence Margin =", 100*margin, "%\n")

  if (ci[1] >= -margin && ci[2] <= margin) {
    cat("Equivalence Established! (Significance Level =", 100*alpha, "%)\n\n")
  } else cat("Equivalence NOT Established. (Significance Level =", 100*alpha, "%)\n\n")

  cat("(Assumption: 1st Trial is New, 2nd one is Current (Reference), and Higher Proportion is Better.)\n")
  if (ci[1] >= -margin) {
    cat("Noninferiority Established! (Significance Level =", 100*alpha, "%)\n\n")
  } else cat("Noninferiority NOT Established. (Significance Level =", 100*alpha, "%)\n\n")


  ## Sample Size Determination (TOST) 
  p <- x/n
  c1 <- ((qnorm(0.95) + qnorm(0.8)))^2  # Type I Error = 5%, Type II Error = 20%, Power = 80%
  pd <- abs(pdiff)
  if (pd >= margin) N <- NA else N <- ceiling(c1 * (p[1]*(1-p[1])+p[2]*(1-p[2])) / (pd - margin)^2 )
  cat("Sample Size Required (using only input proportions and margin) =", N, "(Power = 80 % )\n")

  plot(0, 0, xlim=c(-2*margin, 2*margin), ylim=c(-1,1), axes=F, xlab="Difference in Efficacies", ylab="", type="n")
  axis(side=1, at=c(-2*margin, -margin, 0, margin, 2*margin), labels=c("", paste("-",
                                                                100*margin, "%"), "0",
                                                                paste(100*margin, "%"), ""))
  abline(v=c(-margin, 0, margin), lty=c(2,1,2))
  lines(ci, c(0,0), lwd=3)
  lines(rep(ci[1], 2), c(-0.1, 0.1), lwd=2)
  lines(rep(ci[2], 2), c(-0.1, 0.1), lwd=2)
  lines(rep(pdiff, 2), c(-0.1, 0.1), lwd=4)
}
if (F) {
    prop.equiv.tost.test(c(80, 90), c(100,100))
    prop.equiv.tost.test(c(143, 144), c(281,281), margin=0.12, alpha=0.025) 
}

Replace NA value with the last numeric value in each row

replace.NA.with.last.value.in.each.row <- function(dat)
{ 
    ## Purpose: Replace NA value with the last numeric value in each row. 
    ## Arguments:
    ##   dat: a data frame that may have NA in the tail of each row. 
    ## Return: an updated data frame with no NA values. 
    ## Author: Feiming Chen, Date:  3 Jan 2018, 11:34
    ## ________________________________________________

    last.value <- apply(dat, 1, function(x) as.numeric(tail(na.omit(x), 1))) # last numeric value in each row. 

    n <- is.na(dat)
    for (i in 1:nrow(dat)) {
        dat[i, n[i,]] <- last.value[i]
    }

    dat
}
if (F) {                                # Unit Test
    dat <- data.frame(ID=LETTERS[1:5], V1=c(1:4, NA), V2=c(6:7, NA, NA, NA), V3 = c(8, rep(NA, 4)))
    ##   ID V1 V2 V3
    ## 1  A  1  6  8
    ## 2  B  2  7 NA
    ## 3  C  3 NA NA
    ## 4  D  4 NA NA
    ## 5  E NA NA NA
    replace.NA.with.last.value.in.each.row(dat)
    ##   ID V1 V2 V3
    ## 1  A  1  6  8
    ## 2  B  2  7  7
    ## 3  C  3  3  3
    ## 4  D  4  4  4
    ## 5  E NA NA NA
}

Make a combined data frame with a source label using the list names

rbind.df.with.list.names <- function(obj)
{ 
    ## Purpose: Make a combined data frame with a source label using the list names. 
    ## Arguments:
    ##    obj: It is a list of data frames to be "rbind" together. 
    ## Return: a single combined data frame with all the sub data frames in "obj"
    ##         with an addtional column "SOURCE0" from the names of the list "obj",
    ##         and another addtional column "SOURCE1" that abbreviates "SOURCE0". 
    ## Author: Feiming Chen, Date:  2 Jan 2018, 11:00
    ## ________________________________________________

    o <- do.call(rbind, obj)
    o$SOURCE0 <- rep(names(obj), sapply(obj, nrow))
    o$SOURCE1 <- abbreviate(o$SOURCE0)
    o
}
if (F) {                                # Unit Test
    obj <- list(A = data.frame(x = 1:3), B = data.frame(x = 4:6))
    rbind.df.with.list.names(obj)
##     x SOURCE0 SOURCE1
## A.1 1       A       A
## A.2 2       A       A
## A.3 3       A       A
## B.1 4       B       B
## B.2 5       B       B
## B.3 6       B       B
}